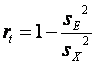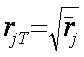Надійність тесту
Admin (Обговорення • внесок) |
Admin (Обговорення • внесок) |
||
| Рядок 13: | Рядок 13: | ||
[[Файл:3_8_004.gif]] | [[Файл:3_8_004.gif]] | ||
| − | + | Кореляція R JT J-го завдання з істинними тестовими балами T пов'язана із середнім значенням його кореляції з іншими завданнями тесту | |
| − | + | ||
| + | [[Файл:3_8_006.gif]] | ||
| + | |||
Якщо тест містить завдання з високою внутрішньою кореляцією, то він буде високо надійним і помилка вимірів буде низькою. | Якщо тест містить завдання з високою внутрішньою кореляцією, то він буде високо надійним і помилка вимірів буде низькою. | ||
Визначення надійності тесту необхідно виконувати на спеціально підібраною вибірці піддослідних, репрезентативно представляє всю генеральну сукупність. Вибірка повинна бути досить великою - 200-300 чоловік. Чим більше вибірка, тим точніше визначається надійність тесту. | Визначення надійності тесту необхідно виконувати на спеціально підібраною вибірці піддослідних, репрезентативно представляє всю генеральну сукупність. Вибірка повинна бути досить великою - 200-300 чоловік. Чим більше вибірка, тим точніше визначається надійність тесту. | ||
| Рядок 33: | Рядок 35: | ||
Наведемо формулу для розрахунку коефіцієнта надійності при двократному тестуванні (паралельному або повторному) | Наведемо формулу для розрахунку коефіцієнта надійності при двократному тестуванні (паралельному або повторному) | ||
| + | [[Файл:3_8_008.gif]] | ||
X I та Y I - індивідуальні бали i -го випробуваного в першому і в другому тестуваннях; N -кількість випробуваних; | X I та Y I - індивідуальні бали i -го випробуваного в першому і в другому тестуваннях; N -кількість випробуваних; | ||
| − | + | ||
| + | Оцінка довірчого інтервалу | ||
Надійність тесту визначає помилку вимірювання індивідуального бала випробуваного, що дозволяє знайти стандартну помилку вимірювання | Надійність тесту визначає помилку вимірювання індивідуального бала випробуваного, що дозволяє знайти стандартну помилку вимірювання | ||
| − | Розглянемо приклад. | + | Розглянемо приклад. Припустимо, що нами було обчислено стандартне відхилення S X = 2,214. Коефіцієнт надійності, розрахований за формулою Спірмена-Брауна, дорівнює R T = 0, 725. Тоді, для стандартної помилки виміру отримаємо |
Знайдемо оцінку довірчого інтервалу для довірчої ймовірності a = 0,05. Припустимо, що середина довірчого інтервалу збігається з X I , а не з T I . Це, звичайно, не так, але ми припустимо, що спостережуваний і істинний тестовий бали не сильно відрізняються. Це цілком справедливо для надійних тестів. Наше припущення приведе до зрушення кордонів довірчого інтервалу, що викличе помилку у визначенні області локалізації істинного тестового бала. | Знайдемо оцінку довірчого інтервалу для довірчої ймовірності a = 0,05. Припустимо, що середина довірчого інтервалу збігається з X I , а не з T I . Це, звичайно, не так, але ми припустимо, що спостережуваний і істинний тестовий бали не сильно відрізняються. Це цілком справедливо для надійних тестів. Наше припущення приведе до зрушення кордонів довірчого інтервалу, що викличе помилку у визначенні області локалізації істинного тестового бала. | ||
Версія за 20:27, 28 жовтня 2012
Найважливішою характеристикою тесту є його надійність, визначальна відтворюваність результатів тестування, їх точність. Припустимо, у нас є гіпотетична група випробовуваних, які негайно забувають зміст тесту по його завершенні. Тоді, у разі надійного тесту, повторюючи тестування багаторазово, ми повинні отримувати одні й ті ж індивідуальні бали. Для малонадійними тесту результати будуть мінятися кожен раз. Тест являє собою систему завдань. Якість завдань визначає надійність тесту в цілому. Розглянемо приклад. Припустимо, тест складається із завдань в закритій формі, в яких помилково не зазначені правильні відповіді. Слабкі випробувані, не знаючи відповіді, будуть намагатися його вгадати. Сильні випробувані, знаючи правильну відповідь, але не знаходячи його серед запропонованих, так само змушені будуть випадковим чином вибирати будь-який з відповідей. У підсумку, індивідуальні бали будуть являти собою випадкові послідовності, не повторюються в різних сеансах тестування. Відтворюваність тестових балів буде повністю відсутнім і надійність тесту буде близька до нуля.Низька надійність тесту обумовлена низькою якістю тестових завдань. Для визначення надійності реальних тестів можна використовувати коефіцієнт кореляції Пірсона для індивідуальних балів різних сеансів тестування. Для організації різних сеансів тестування можна використовувати або паралельні тести, або повторне тестування через певний проміжок часу. Можна також використовувати результати одного сеансу тестування. При цьому виконують розщеплення тесту, наприклад, на парні і непарні завдання і, потім, знаходять кореляцію між цими двома половинами. Надійність тесту визначається різними методами. Розглянемо їх. З класичної теорії тесту випливає, що надійність тесту є
де S E 2 - дисперсія помилкового внеску тестовий бал, S E 2 - дисперсія спостережуваного тестового бала. Коли помилка відсутня, коефіцієнт надійності дорівнює одиниці. Якщо виміряний тестовий бал повністю обумовлений помилкою вимірювання, то надійність тесту дорівнює нулю. Помилка виміру залежить від надійності тесту R T .
Кореляція R JT J-го завдання з істинними тестовими балами T пов'язана із середнім значенням його кореляції з іншими завданнями тесту
Якщо тест містить завдання з високою внутрішньою кореляцією, то він буде високо надійним і помилка вимірів буде низькою. Визначення надійності тесту необхідно виконувати на спеціально підібраною вибірці піддослідних, репрезентативно представляє всю генеральну сукупність. Вибірка повинна бути досить великою - 200-300 чоловік. Чим більше вибірка, тим точніше визначається надійність тесту. Для обчислення надійності тесту потрібні результати двох випробувань, які організовуються наступними способами: 1-й спосіб - тестування за допомогою двох паралельних тестів (parallel-form reliability); 2-й спосіб - повторне тестування за допомогою одного і того ж тесту (test-retest reliability); 3-й спосіб - розщеплення тесту (split-half method).
Перший спосіб, мабуть, найкращий, з погляду розрахунку надійності. Основною проблемою тут є розробка паралельних тестів. Вкрай складно створити тести паралельні і за змістом і за результатами. Раніше нами наводився приклад «паралельних» завдань, що дають різні результати: 6 + 3 = ____; 6 + ___ = 9; ___ + 3 = 9.
Другий спосіб технічно набагато простіше, проте тут з'являються нові фактори. По-перше, перше тестування змінює рівень підготовленості випробуваних. Це може відбутися з різних причин, зокрема, запам'ятовування завдань тесту. Тому повторне тестування необхідно проводити через деякий інтервал часу. Цей інтервал має бути якомога більше. По-друге, до моменту повторного тестування змінюються зовнішні умови - інші соціальне середовище, інші взаємодії з членами мікросоціальної групи, іншу пору року, і т.д.Крім того, змінилися і самі піддослідні, змінився їх рівень знань як спеціальних, так загальнокультурних. В результаті повторне тестування проводиться в інших умовах і іншій групі випробуваних. У зв'язку з цим бажано часовий інтервал між тестуваннями вибирати як можна коротше. Ми отримали взаємовиключні вимоги до інтервалу повтору тестування, отже, тут доведеться йти на компроміс. Можна рекомендувати інтервал в один місяць, хоча подібні рекомендації повинні підтверджуватися експериментально.
Треба усвідомлювати, що повторне тестування в силу зазначених причин, в принципі не дозволяє отримати паралельні результати навіть для ідеального тесту з надійністю рівній одиниці.
Третій спосіб дуже простий. На підставі всього лише одного тестування ми можемо оцінити надійність тесту. Отримані результати тим або іншим способом діляться на дві групи. Наприклад, у першу входять результати по парних завданнях, у другу - результати по непарних завдань. Потім обчислюється коефіцієнт кореляції між цими групами.Недолік цього способу обумовлений неідентичність цих груп.
Наведемо формулу для розрахунку коефіцієнта надійності при двократному тестуванні (паралельному або повторному)
 X I та Y I - індивідуальні бали i -го випробуваного в першому і в другому тестуваннях; N -кількість випробуваних;
X I та Y I - індивідуальні бали i -го випробуваного в першому і в другому тестуваннях; N -кількість випробуваних;
Оцінка довірчого інтервалу
Надійність тесту визначає помилку вимірювання індивідуального бала випробуваного, що дозволяє знайти стандартну помилку вимірювання
Розглянемо приклад. Припустимо, що нами було обчислено стандартне відхилення S X = 2,214. Коефіцієнт надійності, розрахований за формулою Спірмена-Брауна, дорівнює R T = 0, 725. Тоді, для стандартної помилки виміру отримаємо
Знайдемо оцінку довірчого інтервалу для довірчої ймовірності a = 0,05. Припустимо, що середина довірчого інтервалу збігається з X I , а не з T I . Це, звичайно, не так, але ми припустимо, що спостережуваний і істинний тестовий бали не сильно відрізняються. Це цілком справедливо для надійних тестів. Наше припущення приведе до зрушення кордонів довірчого інтервалу, що викличе помилку у визначенні області локалізації істинного тестового бала.
Помилка, що допускається при цьому, виходить прийнятною. Тоді половина довірчого інтервалу дорівнює
δ X I = 1,96 S E = 1,96 × 1,161 = 2,27 Тепер знайдемо кордону тестового бала, наприклад, для другого випробуваного X 2 = 6 (таблиця 3.8.2). Мінімальне значення одно 6-2,27 = 3,73 ≈ 4. Максимальне дорівнює 6 +2,27 = 8,27 ≈ 8. Отже, істинний бал випробуваного № 2 знаходиться в проміжку від 4 до 8 балів.
Як бачимо, питання визначення надійності тесту, необхідно приділяти найпильнішу увагу. Створений на швидку руку «тест» - таким не є. Це всього лише сукупність завдань.У кращому випадку, це сукупність завдань у тестовій формі . Тільки статистична перевірка тесту дозволяє перетворити його в систему тестових завдань . Тільки вказівку його надійності , дозволяє адекватно трактувати результати тестування. Таким чином, питання визначення надійності тесту, його стандартної помилки, області локалізації істинного тестового бала дуже важливі для створення якісного педагогічного тесту і його подальшої сертифікації.